Orbital
(updated 2024-12-30)
This continues my exploration of JavaScript.
Motivation
Samantha Harvey says her book Orbital tries to be a space pastoral, describing the relationships of six space station astronauts during the sixteen orbits of a single earth day. There is no threatening destruction or steamy romance, just an encounter between Earth and its Anthropocene exhabitants.
The frontispiece of Orbital shows the orbits of the space station during this day; it is fun to think about orbits. For instance, daylight is not restricted to the northern hemisphere!
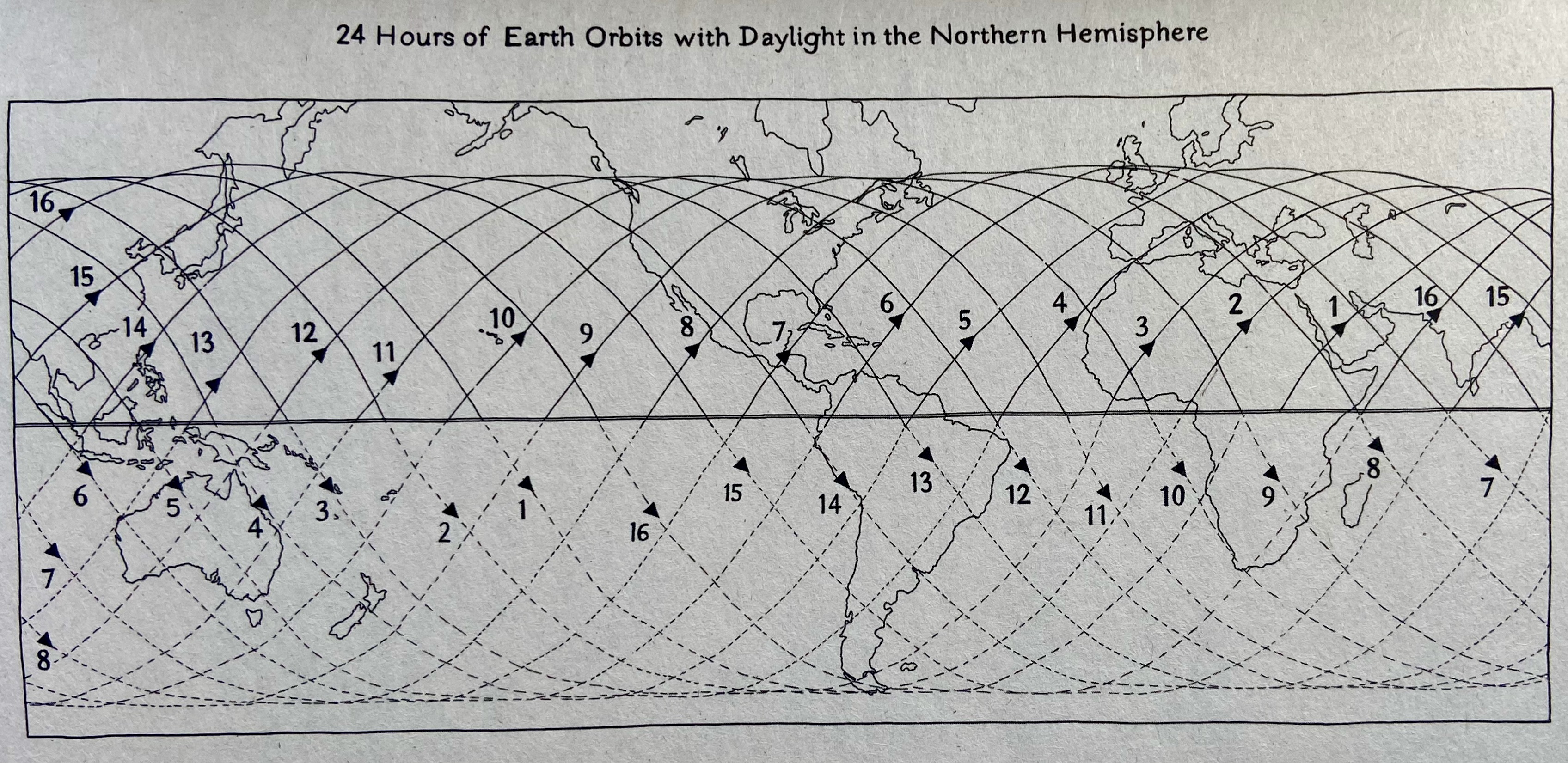
A circular orbit is a path where an object (e.g., space station) moves around a central body (e.g., the earth) in a perfect circle. An equatorial orbit is an orbit that is directly above the equator. An inclined orbit is tilted relative to the equator. The space station has an inclined orbit, where the inclination is 51.6°. This is the angle that each orbit crosses the equator.
If the earth were stationary, the space station would always traverse the globe along a single circumference. But the earth rotates, so each time the space station completes an orbit, its location over the ground has changed. The amount of change is the amount that the earth has rotated during the space station’s orbit. This is why the orbits are offset in the frontispiece above.
The altitude of a satellite orbit occurs when gravitational force pulling the satellite toward the earth is balanced by the centripetal force caused by the speed of the satellite in orbit. Since satellite mass is a linear term in both the gravitational and centripetal equations, the actual mass of the satellite does not determine orbit. Geostationary satellites are much further from the earth (35,800 km) than the space station (in low earth orbit, about 410 km). Satellites in more distance (e.g., geostationary) orbits move slower than satellites closer to the earth (e.g., the space station or StarLink communication satellites) because satellites closer to the earth have to overcome the stronger force of Earth’s gravity.
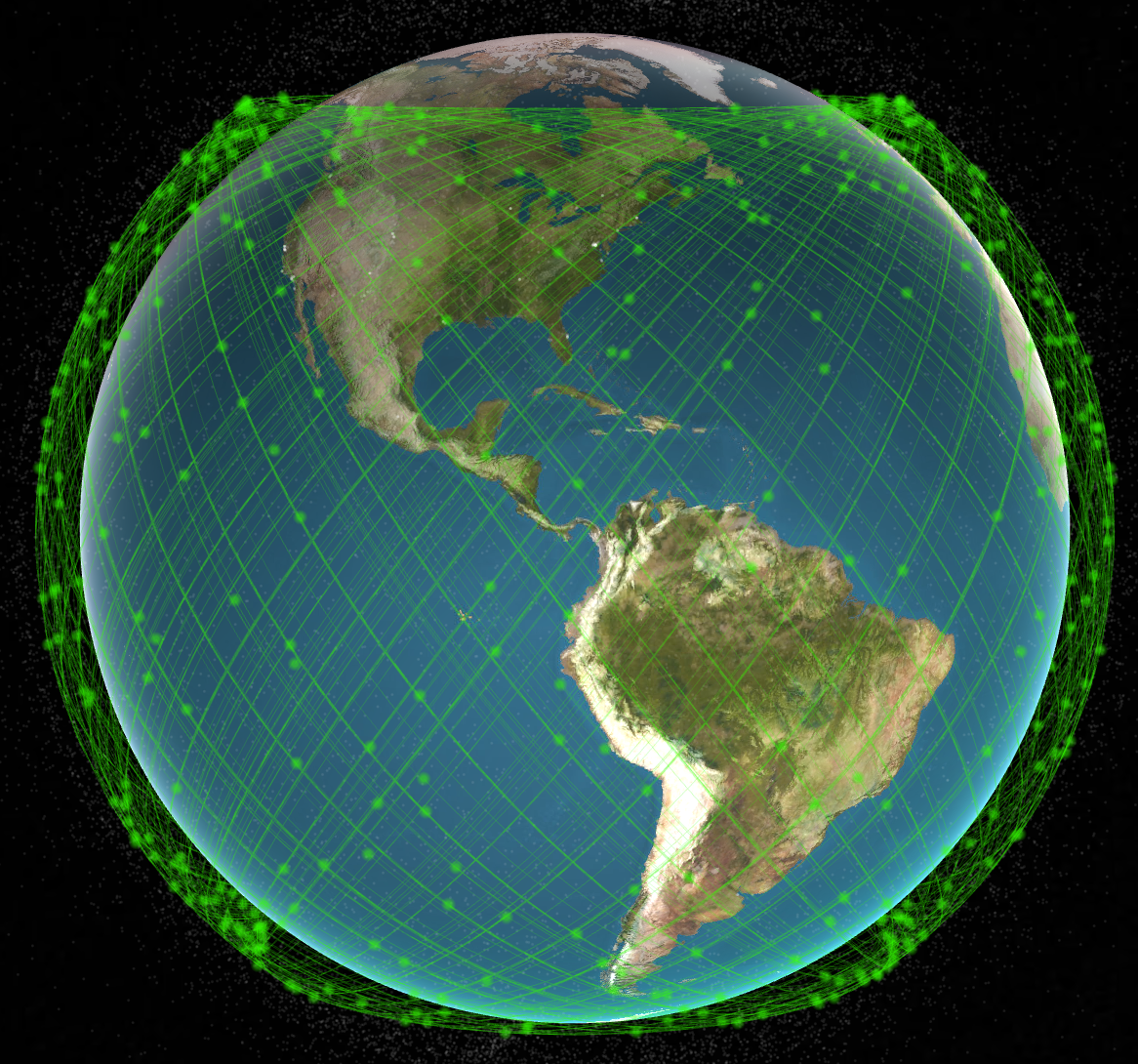
There are a lot of satellites (and other objects) in space. Here are the almost 7,000 Starlink satellites.
Math
This answer on the Space Exploration StackExchange provides basic math required. There are three steps.
The first step is to describe movement on a sphere with an inclined orbit.
where the radius of the orbit is 1, \(\omega = 2 \pi / T\) is the circumference of the sphere scaled by the orbital period \(T\), and \(i\) the inclination of the orbit. \(t\) is the time since the start of the orbit.
The next step is to translate the three-dimensional coordinates to two-dimensional latitude and longitude. These equations assume that the orbit starts at longitude 0.
Incorporate the rotation of the earth by subtracting the scaled orbital period of the earth; only the longitude is influenced by the rotating earth.
\(\omega_E = 2 \pi / T_E\) and \(T_E\) is the orbital period of the earth.
We use minutes as the unit of time. The orbital period of the space station \(T\)varies between 90 and 93 minutes; we’ll use 92 minutes. The orbital period of the earth \(T_E\) is approximately 1436 minutes (23 hours 56 minutes and 4 seconds). The inclination of the space station orbit is approximately 51.6°.
A more realistic calculation might use two-line element set notation to characterize the location and movement of a satellites at a particular point in time, coupled with simplified perturbation models to calculate orbital state vectors. satellites-js or ootk are two JavaScript implementations.
Orbital
The first sketch show a flattened earth, with space station orbits superimposed. The orbits are described by equations for \(lat, lon\) from the previous section. The orbits appear offset in space. But actually the orbits are constant, it is the earth that rotates under the space station. The space station dots are equally spaced in time, but a close observation shows that they are further apart at the largest latitudes; this is because the projection of the spherical earth into two dimensions stretches larger latitudes more than smaller latitudes.
The second sketch shows the rotating earth, inclined 23.5°. The space station orbit is constant, always intersecting the equator in the middle of the image. The location of the space station is described the equations for \(x, y, z\) above. The orbit is inclined 51.6° from the equator. Space station markers move to the right in synchrony with the rotating earth; it took me a long time to figure out how to make this simple transformation in p5!. The earth’s radius is 6378 km, and the orbit is 400 km above the earth. Illumination is from the front and left, as would occur somewhere between the spring (June) solstice and summer (March) equinox; the image of the earth, from NASA, is generated from November data, so is not quite correct.
An abstraction has the earth’s equator, orbit, and the location of the visitor’s internet access. The earth is illuminated from the top so that ‘daylight is in the northern hemisphere’. The space station orbit pulses at 92 beats per minute. The axial tilt of the earth is a little akimbo.
Notes
The implementation uses p5; here’s the JavaScript. I use
‘WEBGL’ mode for 3D rendering. A difference between WEBGL and P2D
rendering is the the WEBGL coordinate system has the center of the
canvas as the origin, versus the top left under P2D. Also objects in
WEBGL are are always centered at 0; locations in the canvas are
determined using operations such as translate() and rotateY() to
adjust the relative coordinate system before drawing the
object. push() and pop() are used to limit the effects of
translate() etc., to sepcific shapes.
This post uses MathJax for rendering mathematical equations; see this helpful StackOverflow post. I used Rodriques’ rotation formula from this StackOverflow answer to rotate the light source around the Earth.